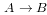
命題の classical logic では、
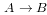
と
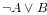
は同値です。つまり前者を後者で定義してもかまいません。しかし、この同値性は classical logic で特別に成り立つものです。例えば、intuitionistic logic では後者から前者を導けますが、前者から後者は導けません。また minimal logic ではいずれも導けません。
では classical logic における同値性の証明はどのようになるでしょうか。Natural deduction による証明が以下です。
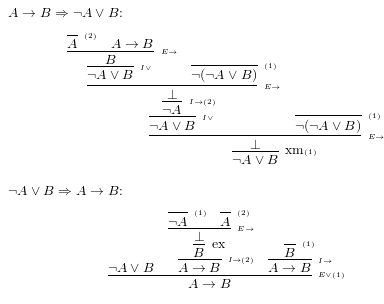
上の段にある前者から後者の証明は、xm (the law of excluded middle)を使っています。
下の段にある後者から前者の証明は、ex (the principle of explosion)を使っています。しかし xm は使っていません。このため、これは intuitionistic logic での証明にもなっています。