古典命題論理では、予め決められた有限個の論理変数が与えられたときに、論理記号\(\land\)("and")、\(\lor\)("or")、および\(\neg\)("not")を用いた論理式で書ける条件の数は簡単に数えることが出来ます。ただし、条件を数えるときには同値な論理式は区別しません。与えられた論理変数の個数を\(n (> 0)\)とすると、論理式は\(n\)引数のブール関数に対応するという事実から、ちょうど\(2^{2^n}\)個の条件が表せます。実際には、用いる論理記号には\(\land\)と\(\neg\)だけ(あるいは、\(\lor\)と\(\neg\)だけ)で十分であることは、ド・モルガン則からすぐ分かります。
では、論理記号に\(\land\)と\(\lor\)だけを用いると制限する場合はどうでしょうか?
\(n=1\)なら、\(\land\)も\(\lor\)も羃等なのでその論理変数そのものからなる式1つだけです。
\(n=2\)なら、与えられた変数をPおよびQとすると、
\(n=3\)なら、与えられた変数をP、Q、およびRとして、次のベン図とともに示される18個の式で全部です。
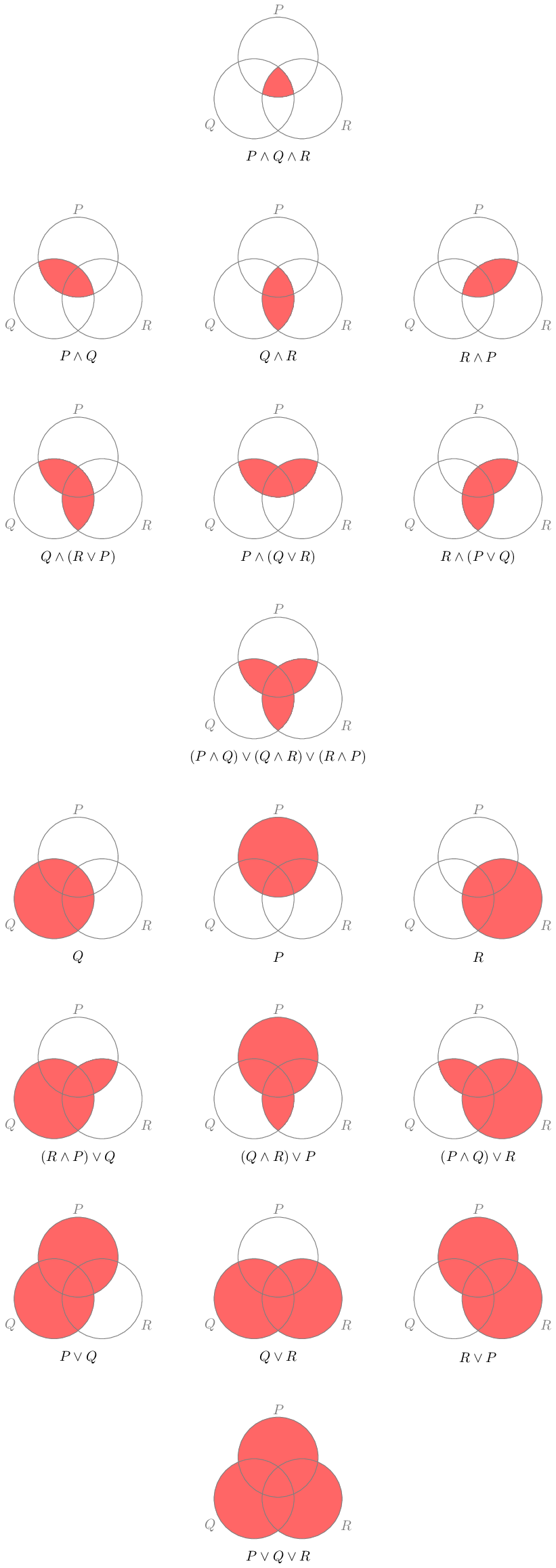
実は、任意の自然数\(n\)について\(\land\)と\(\lor\)を用いて表現可能な非同値な論理式の数\(N(n)\)を具体的に計算するという問題は未解決です。なぜなら、そのような数が具体的に挙げられる場合、\(n\)個の変数に依存するmonotone boolean functionの数\(M(n)\)を数えられることになるからです。Monotone boolean functionとしては\(\top\)(恒真)および\(\bot\)(恒偽)に当たる2つを加えることになるため、\(M(n) = N(n)+2\)と計算できます。この\(M(n)\)はデデキント数と呼ばれ、\(n \leq 8\)の場合しか具体的な数字が知られていません。